Determinan memiliki banyak kegunaan. Bukan hanya untuk menyelesaikan suatu sistem persamaan linear, tetapi juga untuk menentukan luas suatu segitiga pada bidang koordinat. Perhitungan luas segitiga dengan determinan digunakan jika posisi titik-titik sudut segitiga diketahui.
Teorema
Bukti
Perhatikan segitiga ABC dengan koordinat $A(x_1 , y_1)$, $B(x_2 , y_2)$, dan $C(x_3 , y_3)$ berikut.
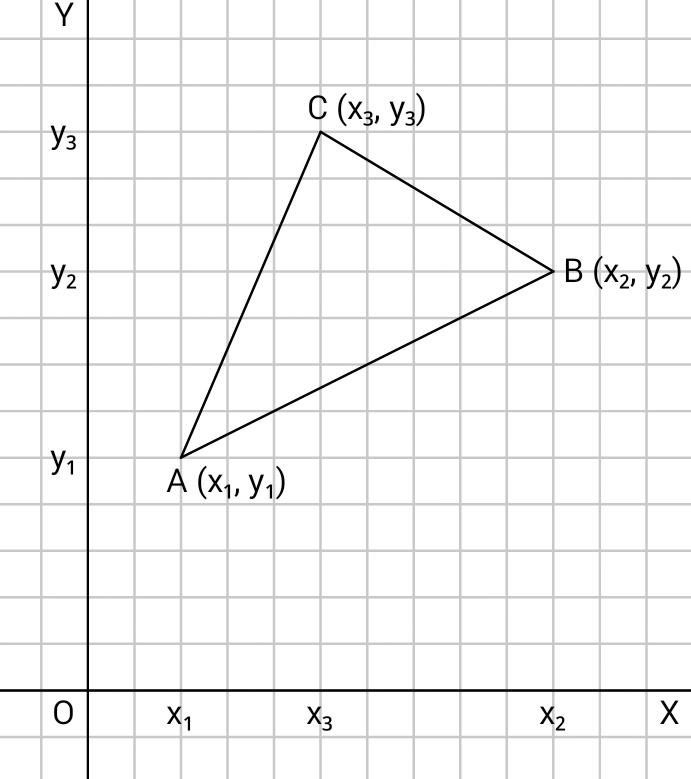
Selanjutnya, kita menggambar persegi panjang yang melalui ketiga titik sudut segitiga.
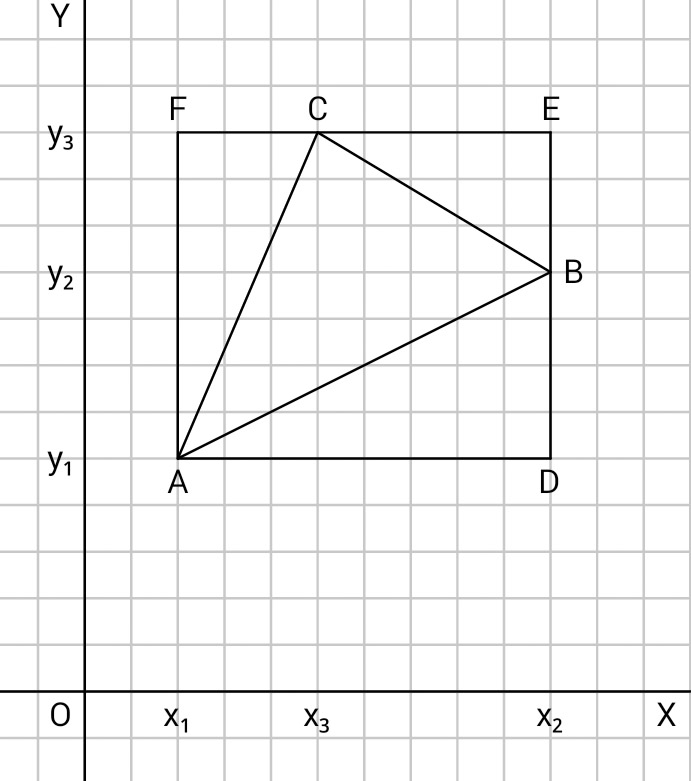
Melalui pengamatan gambar, kita memperoleh$$\begin{aligned}\text{AD} &= x_2-x_1 \\\text{BD} &= y_2-y_1 \\\text{BE} &= y_3-y_2 \\\text{CE} &= x_2-x_3 \\\text{CF} &= x_3-x_1 \\\text{AF} &= y_3-y_1\end{aligned}$$

Kemudian, kita mencari luas daerah persegi panjang $\text{ADEF}$ dan luas segitiga-segitiga, selain segitiga $\text{ABC}$.
$$\begin{aligned}\text{L ABCD} &= \text{AD} \cdot \text{AF} = (x_2-x_1)(y_3-y_1) = x_2 y_3-x_2 y_1-x_1 y_3 + x_1 y_1 \\\text{L }\triangle \text{ADB} &=\frac{1}{2} \text{AD} \cdot \text{BD} =\frac{1}{2} (x_2-x_1)(y_2-y_1)=\frac{1}{2}(x_2 y_2-x_2 y_1-x_1 y_2 + x_1 y_1) \\\text{L } \triangle \text{BEC} &=\frac{1}{2} \text{CE} \cdot \text{BE} =\frac{1}{2} (x_2-x_3)(y_3-y_2)=\frac{1}{2}(x_2 y_3-x_2 y_2-x_3 y_3 + x_3 y_2) \\\text{L } \triangle \text{ACF} &= \frac{1}{2} \text{CF} \cdot \text{AF} =\frac{1}{2} (x_3-x_1)(y_3-y_1)=\frac{1}{2}(x_3 y_3-x_3 y_1-x_1 y_3 + x_1 y_1)\end{aligned}$$
Jumlahkan luas ketiga segitiga tersebut, sehingga diperoleh$$\text{L } \triangle \text{ADB} + \text{L } \triangle \text{BEC} + \text{L } \triangle \text{ACF} = x_1 y_1 + \frac{1}{2} (x_2 y_3 + x_3 y_2-x_2 y_1-x_1 y_2-x_3 y_1-x_1 y_3)$$
Untuk menghitung luas segitiga $\text{ABC}$, kurangi luas $\text{ABCD}$ dengan jumlah luas ketiga segitiga lainnya.$$\begin{aligned}\text{L } \triangle \text{ABC} &= (x_2 y_3-x_2 y_1-x_1 y_3 + x_1 y_1)-[x_1 y_1 + \frac{1}{2} (x_2 y_3 + x_3 y_2-x_2 y_1-x_1 y_2-x_3 y_1-x_1 y_3] \\&= \frac{1}{2} x_2 y_3-\frac{1}{2} x_2 y_1-\frac{1}{2} x_1 y_3-\frac{1}{2} x_3 y_2 + \frac{1}{2} x_1 y_2 + \frac{1}{2} x_3 y_1\end{aligned}$$
Melalui proses penyederhanaan, kita memperoleh$$\text{L } \triangle \text{ABC} = \frac{1}{2} [(x_2 y_3-x_3 y_2)-(x_1 y_3-x_3 y_1) + (x_1 y_2-x_2 y_1)$$
Perhatikan bahwa $x_2 y_3-x_3 y_2$ merupakan determinan dari matriks$$\left[\begin{array}{rr}x_2 & y_2\\x_3 & y_3\end{array}\right]$$
Sehingga kita dapat menuliskan$$x_2 y_3-x_3 y_2=\left|\begin{array}{rr}x_2 & y_2\\x_3 & y_3\end{array}\right|$$
Dengan cara yang sama, kita bisa menuliskan dua suku lainnya sebagai determinan suatu matriks. Sehingga luas segitiga ABC menjadi$$\text{L } \triangle \text{ABC} = \frac{1}{2} \left(\left|\begin{array}{rr}x_2 & y_2\\x_3 & y_3\end{array}\right|-\left|\begin{array}{rr}x_1 & y_1\\x_3 & y_3\end{array}\right| + \left|\begin{array}{rr}x_1 & y_1\\x_2 & y_2\end{array}\right|\right)$$
Perhatikan bahwa$$\left|\begin{array}{rr}x_2 & y_2\\x_3 & y_3\end{array}\right|-\left|\begin{array}{rr}x_1 & y_1\\x_3 & y_3\end{array}\right| + \left|\begin{array}{rr}x_1 & y_1\\x_2 & y_2\end{array}\right|$$merupakan determinan dari suatu matriks $M$, dengan$$M = \left[\begin{array}{rrr} x_1 & y_1 & 1\\x_2 & y_2 & 1\\x_3 & y_3 & 1\end{array}\right]$$
Jadi, rumus luas segitiga ABC menjadi$$\text{L } \triangle \text{ABC} = \frac{1}{2} [det(M)]= \frac{det(M)}{2}$$
Penukaran posisi dua baris akan mengubah tanda determinan. Jadi, untuk mengantisipasi munculnya luas yang bernilai negatif, kita perlu menambahkan tanda nilai mutlak pada rumus di atas. Diperoleh$$L \triangle ABC = \left| \frac{det(M)}{2} \right|$$Terbukti.
Contoh
Hitunglah luas segitiga dengan titik-titik sudut $(3, 3)$, $(4, 0)$, $(-2, -1)$.
Pembahasan
Pertama, kita bentuk matriks $M$ dari koordinat titik-titik sudut segitiga tersebut.$$M = \left[\begin{array}{rrr} 3 & 3 & 1\\4 & 0 & 1\\-2 &-1& 1\end{array}\right]$$
Berikutnya, kita menghitung determinan matriks $M$. Kita menggunakan ekspansi kofaktor sepanjang baris kedua.$$\begin{aligned}\text{det}(M) &= -4 \left| \begin{array}{rr} 3 & 1\\ -1 &1\end{array} \right|+0 \left| \begin{array}{rr} 3 & 1\\ -2 &1\end{array} \right|-1 \left| \begin{array}{rr} 3 & 3\\ -2 &-1\end{array} \right| \\&= -4 \cdot (3-(-1))+0-(-3-(-6)) \\&= -4 \cdot 4-3 \\&= -16-3 \\&= -19\end{aligned}$$
Berikutnya, kita menghitung luas segitiga dengan rumus$$\text{L } \triangle \text{ABC} = \left| \frac{det(M)}{2} \right| = \left| \frac{-19}{2} \right| = \frac{19}{2}$$Jadi, luas segitiga ABC adalah $\frac{19}{2}$ satuan luas.
