Dalam tulisan ini, kita akan mengulas cara mencari tinggi segitiga. Bahasan ini tidak dibatasi pada segitiga tertentu saja. Kita akan membahas mengenai tinggi segitiga secara umum, termasuk tinggi segitiga sembarang.
Sebelum membahas lebih lanjut, mari perhatikan daftar isi berikut.
Daftar Isi
Apa Itu Tinggi Segitiga?
Pada segitiga, dikenal istilah garis tinggi. Garis tinggi adalah panjang ruas garis yang ditarik dari titik sudut segitiga dan tegak lurus terhadap garis yang memuat sisi di depannya. Panjang ruas garis inilah yang disebut tinggi segitiga.
Segitiga mempunyai tiga titik sudut, sehingga terdapat tiga garis tinggi. Pada segitiga lancip dan siku-siku, ketiga garis tinggi berada di dalam segitiga. Namun, pada segitiga tumpul, terdapat garis tinggi yang terletak di luar segitiga.
Sebagai contoh, perhatikan segitiga tumpul berikut.
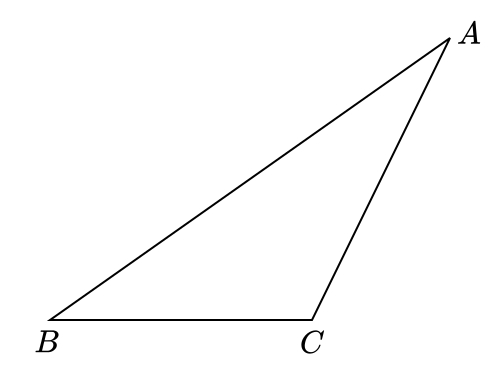
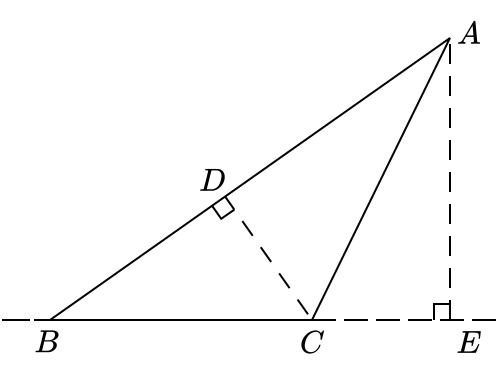
Pada segitiga di atas, CD adalah ruas garis yang melalui titik sudut C dan tegak lurus terhadap garis yang memuat sisi AB (sisi di depan titik C). Artinya, CD adalah garis tinggi segitiga ABC.
Pada segitiga yang sama, AE adalah ruas garis yang melalui titik sudut A dan tegak lurus terhadap garis yang memuat sisi BC (sisi di depan titik A). Artinya, AE juga garis tinggi segitiga ABC. Perhatikan bahwa garis tinggi ini terletak di luar segitiga ABC.
Segitiga ABC mempunyai satu garis tinggi lagi. Bisakah anda menggambarnya?
Prosedur untuk mencari tinggi segitiga bergantung pada jenis dan komponen-komponen segitiga yang diketahui, seperti besar sudut dan panjang sisi. Pada bagian berikutnya, kita akan membahas prosedur mencari tinggi segitiga, jika diketahui panjang ketiga sisi segitiga.
Tinggi Segitiga Sama Sisi
Bagaimana Mencari Tinggi Segitiga Sama Sisi?
Segitiga sama sisi adalah segitiga yang ketiga sisinya sama panjang. Pada segitiga sama sisi, ketiga garis tinggi mempunyai panjang yang sama. Jika panjang sisinya adalah $a$ maka tinggi segitiga tersebut adalah $\frac{1}{2}a\sqrt{3}$.
Untuk membuktikan rumus ini, perhatikan segitiga sama sisi berikut.
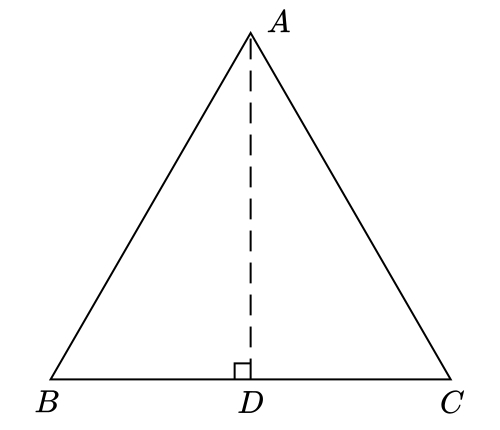
Jika panjang sisi segitiga ABC adalah $AB=BC=CA=a$, maka panjang ruas garis BD adalah $a/2$. Tinggi segitiga ABC adalah AD. Untuk menghitung panjang AD, kita menerapkan rumus pythagoras pada segitiga siku-siku ABD.$$BD^2=AB^2-BD^2=a^2-\left(\frac{a}{2}\right)^2=\frac{3}{4}a^2$$Akibatnya, $BD = \frac{1}{2}a\sqrt{3}$.
Contoh Perhitungan Tinggi Segitiga Sama Sisi
Berikut adalah beberapa contoh perhitungan tinggi pada segitiga sama sisi.
Contoh 1
Tentukan tinggi segitiga sama sisi dengan panjang sisi 6.
Panjang sisi segitiga sama sisi tersebuat adalah 6 cm, sehingga luasnya adalah$$\frac{1}{2}\cdot 6 \cdot \sqrt{3}=3\sqrt{3} \textrm{ cm}^2$$
Contoh 2
Tentukan tinggi segitiga sama sisi dengan panjang sisi 10 cm.
Panjang sisi segitiga sama sisi tersebuat adalah 10, sehingga luasnya adalah$$\frac{1}{2}\cdot 10 \cdot \sqrt{3}=5\sqrt{3} \textrm{ cm}^2$$
Tinggi Segitiga Sembarang
Bagaimana Mencari Tinggi Segitiga Sembarang?
Berikut adalah prosedur mencari tinggi segitiga sembarang.
- Tentukan luas segitiga ABC menggunakan Rumus Heron.
- Tinggi segitiga dari titik sudut A, B, dan C secara berturut-turut adalah $2L/a$, $2L/b$, dan $2L/c$.
Untuk membuktikan rumus ini, kita dapat menggunakan rumus luas segitiga yang melibatkan panjang alas dan tinggi segitiga.
Agar lebih sederhana, kita akan menggunakan notasi $t_X$ untuk menyatakan tinggi segitiga dari titik sudut X. Selain itu, pada segitiga ABC, kita menggunakan notasi $a$ untuk menyatakan sisi $BC$, $b$ untuk menyatakan sisi $AC$, dan $c$ untuk menyatakan sisi $AB$.
Pada langkah 1, kita telah memperoleh luas segitiga ($L$) dengan rumus heron. Selain cara ini, luas segitiga juga dapat dihitung dengan rumus $L=1/2 \cdot \textrm{alas} \cdot \textrm{tinggi}$.

Tinggi segitiga yang bersesuaian dengan sisi $BC=a$ adalah $AD=t_A$, sehingga$$L=\frac{1}{2} \cdot a \cdot t_A \quad \implies \quad t_A=\frac{2L}{a}$$
Dengan cara yang sama, kita dapat menghitung nilai $t_B$ dan $t_C$.
Contoh Perhitungan Tinggi Segitiga Sembarang
Berikut adalah beberapa contoh perhitungan tinggi pada segitiga sembarang.
Contoh 1
Tentukan tinggi segitiga sembarang ABC dengan panjang sisi $AB=21$, $BC=20$, dan $AC=13$.
Diketahui $a=BC=20$, $b=AC=13$, dan $c=AB=21$. Pertama, kita hitung luas segitiga menggunakan rumus heron. Setengah keliling dari segitiga ABC adalah$$s=\frac{a+b+c}{2}=\frac{20+13+21}{2}=\frac{54}{2}=27$$sehingga$$\begin{aligned}L &= \sqrt{s(s-a)(s-b)(s-c)} \\&= \sqrt{27(27-20)(27-13)(27-21)} \\&= \sqrt{27 \cdot 7 \cdot 14 \cdot 6} \\&= \sqrt{\textcolor{blue}{27} \cdot \textcolor{green}{7} \cdot 14 \cdot \textcolor{blue}{3} \cdot \textcolor{green}{2}} \\&= \sqrt{\textcolor{blue}{81} \cdot \textcolor{green}{14} \cdot 14} \\&= \sqrt{9^2 \cdot 14^2} \\&= 9 \cdot 14 \\&= 126 \textrm{ satuan luas}\end{aligned}$$
Jadi, tinggi segitiga ABC adalah$$\begin{aligned}t_A &= \frac{2L}{a} = \frac{2 \cdot 126}{20} = 12.6 \\t_B &= \frac{2L}{b} = \frac{2 \cdot 126}{13} = 19.38 \\t_C &= \frac{2L}{c} = \frac{2 \cdot 126}{21} = 12 \\\end{aligned}$$
Contoh 2
Tentukan tinggi segitiga sembarang ABC dengan panjang sisi $AB=15$, $BC=13$, dan $AC=14$.
Diketahui $a=BC=13$, $b=AC=14$, dan $c=AB=15$. Pertama, kita hitung luas segitiga menggunakan rumus heron. Setengah keliling dari segitiga ABC adalah$$s=\frac{a+b+c}{2}=\frac{13+14+15}{2}=\frac{42}{2}=21$$sehingga$$\begin{aligned}L &= \sqrt{s(s-a)(s-b)(s-c)} \\&= \sqrt{21(21-13)(21-14)(21-15)} \\&= \sqrt{21 \cdot 8 \cdot 7 \cdot 6} \\&= \sqrt{7056} \\&= 84 \textrm{ satuan luas}\end{aligned}$$
Dengan demikian, tinggi segitiga ABC adalah$$\begin{aligned}t_A &= \frac{2L}{a} = \frac{2 \cdot 84}{13} = 12.92 \\t_B &= \frac{2L}{b} = \frac{2 \cdot 84}{14} = 12 \\t_C &= \frac{2L}{c} = \frac{2 \cdot 84}{15} = 11.2 \\\end{aligned}$$
Tinggi Segitiga Sama Kaki
Bagaimana Mencari Tinggi Segitiga Sama Kaki?
Berikut adalah sebuah proposisi yang akan memudahkan perhitungan pada bagian ini.
Proposisi 1
Pada segitiga ABC berlaku$$BC \cdot t_A=AC \cdot t_B=AB \cdot t_C$$di mana $t_A$, $t_B$, dan $t_C$ secara berturut-turut menyatakan tinggi segitiga dari titik sudut $A$, $B$, dan $C$.
Bukti Proposisi 1 cukup sederhana. Kita bisa memanfaatkan rumus $L=1/2 \cdot \textrm{alas} \cdot \textrm{tinggi}$. Selamat mencoba! :)
Segitiga sama kaki mempunyai sepasang sisi yang sama panjang. Nah, garis tinggi yang bersesuaian dengan kedua sisi ini juga sama panjang. Perhatikan segitiga sama kaki berikut.
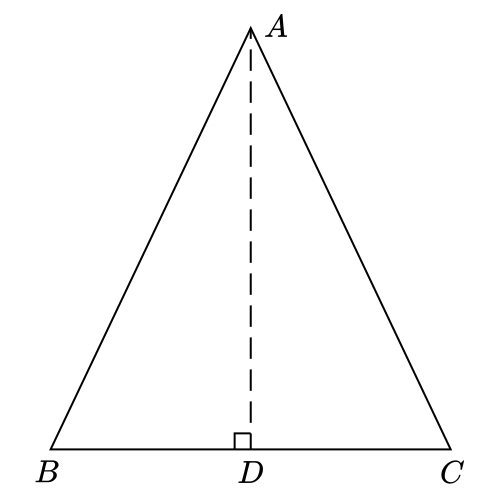
Segitiga ABC adalah segitiga sama kaki, dengan $AB=AC$. Garis tinggi AD membagi sisi BC menjadi dua bagian yang sama panjang, sehingga $BD=BC/2$. Panjang AD dapat dihitung menggunakan rumus pythagoras pada segitiga ABD.
Nah, bagaimana dengan $t_B$ dan $t_C$? Keduanya sama panjang dan dapat dihitung menggunakan Proposisi 1.
Berdasarkan Proposisi 1, diperoleh$$AC \cdot t_B = BC \cdot t_A \quad \implies \quad t_B=\frac{BC \cdot t_A}{AC}$$
Contoh Perhitungan Tinggi Segitiga Sama Kaki
Contoh 1
Tentukan tinggi segitiga ABC dengan panjang sisi $AB=BC=10$ dan $AC=12$.

Panjang BD ($t_B$) dapat dihitung menggunakan rumus pythagoras pada segitiga BCD.$$BD^2=BC^2-CD^2=10^2-6^2=64$$sehingga $t_B=BD=8$.
Panjang sisi AB sama dengan BC, sehingga tinggi segitiga yang bersesuaian dengannya, yaitu $t_A$ dan $t_C$, juga sama panjang.
Berdasarkan Proposisi 1, diperoleh$$\begin{aligned}BC \cdot t_A &= AC \cdot t_B \\10 \cdot t_A &= 12 \cdot 8 \\10 \cdot t_A &= 96 \\t_A &= 9.6\end{aligned}$$
Contoh 2
Tentukan tinggi segitiga ABC dengan panjang sisi $AC=BC=20$ dan $AB=24$.
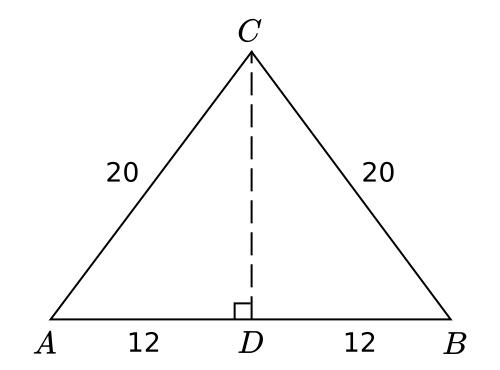
Panjang CD ($t_C$) dapat dihitung menggunakan rumus pythagoras pada segitiga CAD.$$CD^2=AC^2-AD^2=20^2-12^2=256$$sehingga $t_C=CD=16$.
Panjang sisi AC sama dengan BC, sehingga tinggi segitiga yang bersesuaian dengannya, yaitu $t_A$ dan $t_B$, juga sama panjang.
Berdasarkan Proposisi 1, diperoleh$$\begin{aligned}BC \cdot t_A &= AB \cdot t_C \\20 \cdot t_A &= 24 \cdot 16 \\20 \cdot t_A &= 384 \\t_A &= \frac{384}{20} \\&= 19.2\end{aligned}$$
Tinggi Segitiga Siku-Siku
Bagaimana Mencari Tinggi Segitiga Siku-Siku?
Berbeda dengan tiga jenis sebelumnya, segitiga siku-siku merupakan salah satu jenis segitiga berdasarkan besar sudutnya. Segitiga siku-siku adalah segitiga yang mempunyai sebuah sudut siku-siku.
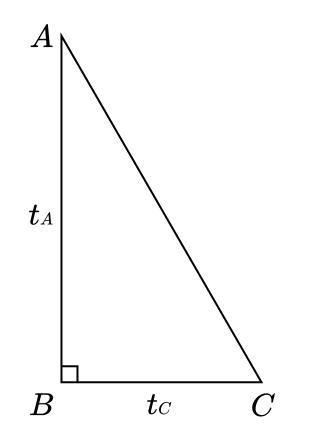
Jika ABC merupakan segitiga siku-siku, dengan $\angle ABC=90 \degree$ (siku-siku di B), maka AB dan BC merupakan garis tinggi segitiga tersebut. Jadi, kita tinggal menentukan panjang garis tinggi yang ketiga, yaitu $t_B$.
Dengan memanfaatkan Proposisi 1, kita dapat menentukan nilai $t_B$, yaitu$$\begin{aligned}AC \cdot t_B &= AB \cdot t_C \\AC \cdot t_B &= AB \cdot BC \\t_B &= \frac{AB \cdot BC}{AC}\end{aligned}$$
Jadi, panjang garis tinggi ini sama dengan hasil kali panjang sisi-sisi tegak dibagi dengan panjang sisi miring.
Contoh Perhitungan Tinggi Segitiga Siku-Siku
Contoh 1
Tentukan tinggi segitiga ABC (siku-siku di C) dengan panjang sisi $AB=10$, $BC=8$, dan $AC=6$.
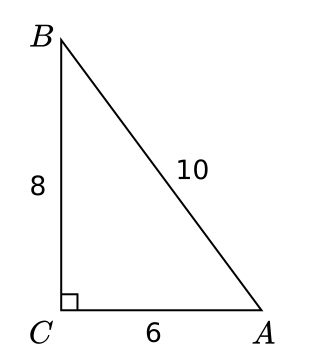
Karena segitiga ABC siku-siku di C, maka $t_A=AC=6$ dan $t_B=BC=8$. Tinggi segitiga dari titik sudut C ($t_C$) adalah$$t_C=\frac{6 \cdot 8}{10}=\frac{48}{10}=4.8$$
Contoh 2
Tentukan tinggi segitiga ABC dengan panjang sisi $AB=10$, $BC=26$, dan $AC=24$.
Karena $26^2=24^2+10^2$, maka segitiga ABC adalah segitiga siku-siku, dengan $\angle CAB=90 \degree$. Secara berturut-turut, tinggi segitiga dari titik sudut B dan C berimpit dengan sisi AB dan AC, sehingga $t_B=AB=10$ dan $t_C=AC=24$. Jika merasa sulit, buatlah sketsa segitiga terlebih dahulu.
Tinggi segitiga dari titik sudut A ($t_A$) adalah$$t_A=\frac{10 \cdot 24}{26}=9.23$$
Bagaimana dengan prosedur menentukan tinggi segitiga lancip dan tumpul? Prosedurnya telah kita bahas :). Segitiga lancip dan tumpul dapat berupa segitiga sama sisi, segitiga sama kaki, atau segitiga sembarang. Identifikasi jenis segitiganya, berdasarkan panjang sisi. Kemudian, ikuti prosedur yang telah kita pelajari.
Segitiga siku-siku dibahas tersendiri, karena ada prosedur yang lebih mudah dalam menentukan panjang garis tingginya.
Semoga bermanfaat! Jika ada yang perlu diperbaiki atau ingin ditanya, sila sampaikan melalui komentar.