Turunan dari suatu penjumlahan fungsi adalah jumlah dari turunan fungsi-fungsi tersebut. Tetapi cara semacam ini tidak berlaku untuk perkalian fungsi. Dalam menentukan turunan hasil kali suatu fungsi, kita tidak mengalikan turunan masing-masing fungsi, tetapi kita menggunakan aturan perkalian. Jika f dan g adalah fungsi yang terdiferensialkan, maka berlaku$$(f \cdot g)' (x) = f'(x)g(x) + g'(x)f(x)$$
Sekarang kita akan membahas pembuktian aturan perkalian pada turunan. Kita akan menggunakan dua cara dalam membuktikan aturan ini. Pertama, menggunakan definisi turunan (berkaitan dengan limit), dan yang kedua menggunakan logaritma natural.
Cara 1
Misalkan f dan g adalah fungsi yang terdiferensialkan, dengan F(x)=f(x)g(x).$$\begin{aligned}F'(x) &= \lim \limits _{h \rightarrow 0} \frac{F(x+h) {}- F(x)}{h} \\&= \lim \limits _{h \rightarrow 0} \frac{f(x+h)g(x+h) {}- f(x)g(x)}{h}\end{aligned}$$
Tambahkan $-g(x+h)f(x)+g(x+h)f(x)$ pada pembilang ruas kanan. Kita juga boleh menambahkan dengan $-f(x+h)g(x) + f(x+h)g(x)$. Hasilnya sama.
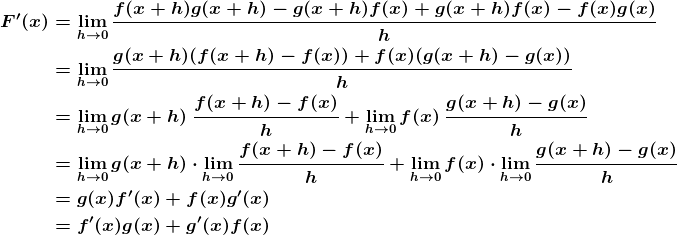
Terbukti. Selanjutnya, kita akan membuktikan aturan perkalian dengan menggunakan logaritma natural.
Cara 2
Misalkan $f$ dan $g$ adalah fungsi yang terdiferensialkan, dengan $F(x)=f(x)g(x)$. Beri logaritma natural pada kedua ruas.$$\ln F(x)=\ln [f(x)g(x)]$$
Ingat sifat logaritma natural $\ln ab = \ln a + \ln b$.$$\ln F(x)=\ln f(x) + \ln g(x)$$
Turunkan kedua ruas dengan menggunakan aturan rantai.$$\begin{aligned}F'(x) \: \frac{1}{F(x)} &= f'(x) \: \frac{1}{f(x)} + g'(x) \: \frac{1}{g(x)} \\&= F(x) (\frac{f'(x)}{f(x)} + \frac{g'(x)}{g(x)})\end{aligned}$$
Ingat $F(x)=f(x)g(x)$.$$F'(x) = f(x)g(x) (\frac{f'(x)}{f(x)} + \frac{g'(x)}{g(x)})$$Selanjutnya, gunakan sifat distributif.$$F'(x) = f'(x) g(x) + g'(x) f(x)$$Terbukti.
