Dalam tulisan ini, kita akan membahas soal Kombinatorika dalam ON MIPA-PT Matematika Tahun 2006. Soal kombinatorika terdiri dari delapan soal isian singkat dan tiga soal uraian. Sebelumnya, kita telah membahas soal isian Kombinatorika tahun 2006. Jadi, sebagai lanjutan tulisan tersebut, kita akan membahas tiga soal uraian yang tersisa.
Nomor 1
Misal $(x_i,y_i,z_i)$, $i=1,2,\cdots,9$, adalah himpunan 9 titik berbeda dengan koordinat bulat pada ruang $xyz$. Tunjukkan bahwa titik tengah dari garis yang menghubungkan sedikitnya satu pasang dari titik-titik tersebut berkoordinat bulat.
Pembahasan
Misalkan a menyatakan bilangan genap dan b menyatakan bilangan ganjil, serta notasi aab menunjukkan bahwa komponen $x$, $y$, $z$ dari suatu titik secara berturut-turut bernilai genap, genap, dan ganjil.
Bentuk himpunan $M$ yang memuat semua komposisi yang mungkin, yaitu$$M=\{ aaa,aab,aba,abb,baa,bab,bba,bbb \}$$Himpunan $M$ memiliki sebanyak 8 anggota. Pada soal di atas, terdapat 9 titik berbeda dengan koordinat bulat. Berdasarkan Prinsip Sangkar Burung (Pigeon Hole Principle), terdapat sedikitnya dua titik yang memiliki komposisi sama.
Misalkan titik tersebut adalah $S=(x_s,y_s,z_s)$ dan $T=(x_t,y_t,z_t)$. Ingat bahwa jumlah dua bilangan genap adalah bilangan genap dan jumlah dua bilangan ganjil adalah bilangan genap. Karena titik $S$ dan $T$ memiliki komposisi yang sama, maka $x_s+x_t$, $y_s+y_t$, dan $z_s+z_t$ merupakan bilangan genap. Tulis$$\begin{aligned}&x_s+x_t=2p \\&y_s+y_t=2q \\&z_s+z_t=2r \\\end{aligned}$$untuk suatu $p,q,r \in \mathbb{Z}$.
Titik tengah $S$ dan $T$ memiliki koordinat bulat, yaitu$$\left( \frac{x_s+x_t}{2}, \frac{y_s+y_t}{2}, \frac{z_s+z_t}{2} \right) = \left( \frac{2p}{2}, \frac{2q}{2}, \frac{2r}{2} \right)=(p,q,r)$$Terbukti.
Nomor 2
Ada $n$ orang akan naik becak (menjadi penumpang) $r$ buah becak berlainan, dengan $n>r>1$, dan setiap becak berisi satu atau dua penumpang. Ada berapa cara memasangkan $n$ orang ke $r$ becak tersebut sehingga setiap becak berisi satu atau dua penumpang?
Pembahasan
Kita akan menyelesaikan soal ini dengan fungsi pembangkit eksponensial. Terdapat sebanyak $r$ becak, yang masing-masing berisi satu atau dua penumpang. Fungsi pembangkit eksponensialnya adalah$$f(x)= \left( x+\frac{x^2}{2!} \right) ^r$$
Jawaban soal ini sama dengan koefisien $\frac{x^n}{n!}$ pada fungsi $f(x)$. Perhatikan bahwa$$\begin{aligned}f(x) &= \left( x+\frac{x^2}{2!} \right) ^r \\&= \left[ x \left( 1+\frac{1}{2}x \right) \right] ^r \\&= x^r \cdot \left( 1+\frac{1}{2}x \right)^r \\&= x^r \cdot \sum_{i=0}^r \binom{r}{i} \cdot \left( \frac{1}{2}x \right) ^i \cdot 1^{r-i} \\&= x^r \cdot \sum_{i=0}^r \binom{r}{i} \cdot \frac{x^i}{2^i}\end{aligned}$$
Suku yang memuat $\frac{x^n}{n!}$ diperoleh jika $i=n-r$, yaitu$$x^r \cdot \binom{r}{n-r} \cdot \frac{x^{n-r}}{2^{n-r}} = \frac{n!}{2^{n-r}} \cdot \binom{r}{n-r} \cdot \frac{x^n}{n!}$$Dengan ini, kita memperoleh koefisien suku yang kita cari. Jadi, banyaknya cara memasangkan $n$ orang ke $r$ becak tersebut sehingga setiap becak berisi satu atau dua penumpang adalah$$\frac{n!}{2^{n-r}} \cdot \binom{r}{n-r}$$
Nomor 3
Tentukan banyak rute terpendek dari kota A ke kota B.

Pembahasan
Perhatikan gambar berikut.
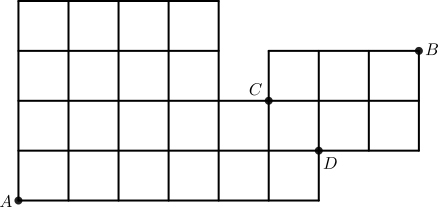
Rute terpendek hanya memungkinan kita bergerak ke kanan atau ke atas. Sehingga rute terpendek dari A ke B pasti melalui salah satu dari titik C dan D.
Pertama, kita menentukan banyaknya rute terpendek yang melalui titik C. Banyak rute terpendek dari A ke C adalah $\binom{7}{2}$, sedangkan banyak rute terpendek dari C ke B adalah $\binom{4}{1}$. Berdasarkan aturan perkalian banyaknya rute terpendek dari A ke B yang melalui titik C adalah$$\binom{7}{2} \cdot \binom{4}{1}=\frac{7!}{5!2!} \cdot \frac{4!}{3!1!}=84$$
Berikutnya, kita menentukan banyaknya rute terpendek yang melalui titik D. Banyak rute terpendek dari A ke D adalah $\binom{7}{1}$, sedangkan banyak rute terpendek dari D ke B adalah $\binom{4}{2}$. Berdasarkan aturan perkalian banyaknya rute terpendek dari A ke B yang melalui titik D adalah$$\binom{7}{1} \cdot \binom{4}{2}=\frac{7!}{6!1!} \cdot \frac{4!}{2!2!}=42$$Jadi, secara keseluruhan, banyaknya rute terpendek dari A ke B adalah $84+42=126$.
Semoga bermanfaat! Jika ada yang perlu diperbaiki atau anda punya solusi yang berbeda, silakan beritahu melalui komentar.
