Persegi panjang adalah bangun datar yang terdiri dari empat sisi. Sisi-sisi yang berhadapan sejajar dan sama panjang, dan keempat sudutnya siku-siku. Persegi panjang memiliki dua dimensi, yang disebut panjang dan lebar. Kedua dimensi ini secara berturut-turut disimbolkan dengan $p$ dan $l$.
Tentu kita tidak asing lagi dengan bangun datar yang satu ini. Karena bentuk persegi panjang sangat sering kita jumpai dalam kehidupan sehari-hari, misalnya pada bangunan. Mulai dari dinding rumah, pintu, sampai perabot sekalipun.
Dalam tulisan ini, kita akan membuktikan rumus luas persegi panjang. Luas persegi panjang diperoleh dengan mengalikan panjang dan lebarnya. Jika dituliskan dalam bentuk simbol, maka$$\text{L} = \text{panjang} \cdot \text{lebar} = p \cdot l$$
Pembuktian Rumus Luas Persegi Panjang
Perhatikan persegi dengan panjang sisi $a+b$ berikut.

Persegi ini dapat dibagi menjadi 4 bangun datar seperti pada gambar berikut.
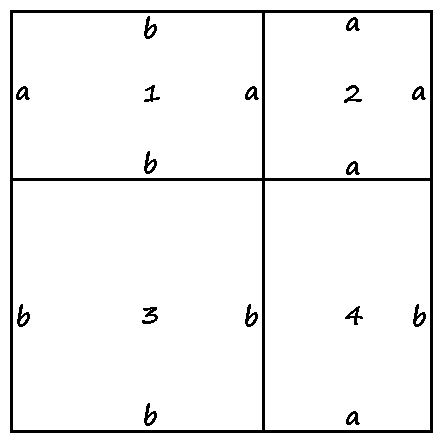
Dari gambar terlihat bahwa persegi yang besar tadi terbagi menjadi dua buah persegi berbeda (Bangun 2 dan 3) dan dua persegi panjang identik (Bangun 1 dan 4).
Luas persegi besar dapat dicari menggunakan rumus $\text{L}=\text{sisi} \cdot \text{sisi}$. Rumus yang sama berlaku pada persegi 2 dengan panjang sisi $a$ dan persegi 3 dengan panjang sisi $b$. Kita akan membuktikan bahwa luas bangun 1 dan 4 sama dengan $a \cdot b$.$$\begin{aligned}\text{L} &= \text{L}_1 + \text{L}_2 + \text{L}_3 + \text{L}_4 \\\left( a + b \right)^2 &= L_1 + a^2 + b^2 + L_4 \\a^2 + b^2 + 2a \cdot b &= L_1 + a^2 + b^2 + L_4\end{aligned}$$
Kedua ruas dikurangi dengan $a^2+b^2$, sehingga diperoleh$$2a \cdot b = \text{L}_1 + \text{L}_4$$
Persegi panjang 1 dan 4 memiliki ukuran yang sama, sehingga luasnya juga sama ($\text{L}_4=\text{L}_1$).$$\begin{aligned}\text{L}_1 + \text{L}_1 &= 2a\cdot b \\2 \cdot \text{L}_1 &= 2a\cdot b \\\text{L}_1 &= a\cdot b\end{aligned}$$
Pada persegi panjang 1, $a$ dan $b$ merupakan panjang dan lebar. Dengan demikian, terbukti bahwa rumus luas persegi panjang adalah$$\text{L} = \text{panjang} \cdot \text{lebar} = p \cdot l$$
