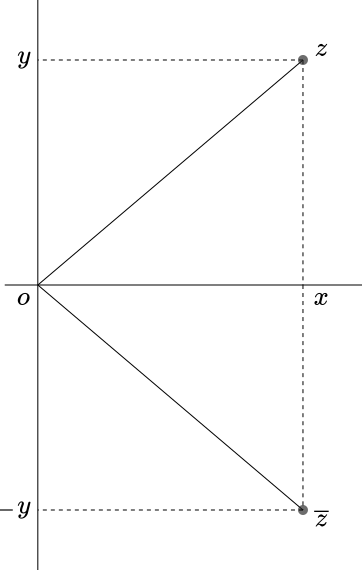
Misalkan $z=(x,y)=x+yi \in \mathbb{C}$. Konjugat dari bilangan kompleks $z$ didefinisikan sebagai $(x,-y)=x-yi$, dengan notasi $\overline{z}$. Konjugat dari $z$ dapat dipandang sebagai hasil pencerminan $z$ terhadap sumbu real pada bidang kompleks. Sebagai contoh, konjugat dari bilangan kompleks $z_1=(-2,5)$ adalah $\overline{z_1}=(-2,-5)$. Dan konjugat dari bilangan kompleks $z_2=3-2i$ adalah $\overline{z_2}=3+2i$.
Berikut adalah beberapa sifat yang berkaitan dengan konjugat dari bilangan kompleks.
Sifat 1
Bukti
Ambil sebarang $z \in \mathbb{C}$. Tulis $z=a+bi$, dengan $a,b \in \mathbb{R}$. Perhatikan bahwa$$\begin{aligned}z &= \overline{z} \\a+bi &= a-bi \\bi &= -bi \\2bi &= 0\end{aligned}$$Kondisi di atas terjadi hanya jika $b=0$. Akibatnya$z=a+0\cdot i=a \in \mathbb{R}$Terbukti.
Sifat 2
BUKTI
Ambil sebarang $z \in \mathbb{C}$. Tulis $z=a+bi$, dengan $a,b \in \mathbb{R}$. Perhatikan bahwa $\overline{z}=a-bi$, sehingga$$\overline{\overline{z}}=a-(-bi)=a+bi=z$$Terbukti.
Sifat 3
BUKTI
Ambil sebarang $z \in \mathbb{C}$. Tulis $z=a+bi$, dengan $a,b \in \mathbb{R}$. Perhatikan bahwa$$z \cdot \overline{z} = (a+bi)(a-bi) = a^2+b^2$$Untuk setiap bilangan real $x$, berlaku $x^2 \geq 0$. Sehingga $a^2 \geq 0$ dan $b^2 \geq 0$, yang berakibat $a^2+b^2 \geq 0$. Jadi$$z \cdot \overline{z} \geq 0$$Terbukti bahwa $z \cdot \overline{z}$ merupakan bilangan real non negatif.
Sifat 4
BUKTI
Ambil sebarang $z_1,z_2 \in \mathbb{C}$. Tulis $z_1=a+bi$ dan $z_2=c+di$, dengan $a,b,c,d \in \mathbb{R}$. Perhatikan bahwa$$z_1+z_2=(a+bi)+(c+di)=(a+c)+(b+d)i$$Sehingga$$\begin{aligned}\overline{z_1+z_2} &= (a+c)-(b+d)i \\&= a+c-bi-di \\&= (a-bi)+(c-di) \\&= \overline{z_1}+\overline{z_2}\end{aligned}$$Terbukti.
Sifat 5
BUKTI
Ambil sebarang $z_1,z_2 \in \mathbb{C}$. Tulis $z_1=a+bi$ dan $z_2=c+di$, dengan $a,b,c,d \in \mathbb{R}$. Perhatikan bahwa$$z_1 \cdot z_2 = (a+bi) \cdot (c+di)=(ac-bd)+(ad+bc)i$$Sehingga$$\begin{aligned}\overline{z_1 \cdot z_2} &= (ac-bd)-(ad+bc)i \\&= (a-bi) \cdot (c-di) \\&= \overline{z_1} \cdot \overline{z_2}\end{aligned}$$Terbukti.
Sifat 6
BUKTI
Ambil sebarang $z \neq 0 \in \mathbb{C}$. Diketahui $z \neq 0$, berarti terdapat $z^{-1} \in \mathbb{C}$ sehingga $z \cdot z^{-1}=1$.
Untuk membuktikan sifat ini, coba perhatikan analogi berikut.
$a$ merupakan invers dari $b$, dan ingin dibuktikan bahwa $a=c$. Ini dapat dilakukan dengan menunjukkan bahwa $c$ juga invers dari $b$. Karena invers bersifat tunggal, maka kedua invers dari $b$ haruslah sama, yaitu $a=c$.
Dalam hal ini, diketahui $\overline{z} \, ^{-1}$ adalah invers dari $\overline{z}$. Untuk menunjukkan bahwa $\overline{z} \, ^{-1}=\overline{z^{-1}}$, kita cukup menunjukkan bahwa $\overline{z^{-1}}$ juga invers dari $\overline{z}$.
Perhatikan bahwa $\overline{z} \cdot \overline{z^{-1}}=\overline{z \cdot z^{-1}}$, berdasarkan sifat 5. Selanjutnya, $z^{-1}$ merupakan invers dari $z$, sehingga$$\overline{z} \cdot \overline{z^{-1}}=\overline{z \cdot z^{-1}}=\overline{1}$$Ingat bahwa konjugat dari bilangan real adalah bilangan real itu sendiri, sehingga $\overline{z} \cdot \overline{z^{-1}}=1$. Artinya $\overline{z^{-1}}$ adalah invers dari $\overline{z}$. Berdasarkan definisi, invers dari $\overline{z}$ adalah invers dari $\overline{z} \, ^{-1}$. Karena invers suatu elemen bersifat tunggal, maka haruslah $\overline{z^{-1}}=\overline{z} \, ^{-1}$.Terbukti.
Sifat 7
BUKTI
Ambil sebarang $z_1,z_2 \in \mathbb{C}$, dengan $z_2 \neq 0$.
Perhatikan bahwa$$\begin{aligned}\overline{\left( \frac{z_1}{z_2} \right)} &= \overline{\left( z_1 \cdot \frac{1}{z_2} \right)} \\&= \overline{\left( z_1 \cdot z_2^{-1} \right)}\end{aligned}$$Berdasarkan sifat 5, diperoleh$$\overline{\left( \frac{z_1}{z_2} \right)} = \overline{\left( z_1 \cdot z_2^{-1} \right)} = \overline{z_1} \cdot \overline{z_2^{-1}}$$Berdasarkan sifat 6, diperoleh $\overline{z_2^{-1}}=\overline{z_2}^{-1}$, sehingga$$\begin{aligned}\overline{\left( \frac{z_1}{z_2} \right)} &= \overline{z_1} \cdot \overline{z_2^{-1}} \\&= \overline{z_1} \cdot \overline{z_2}^{-1} \\&= \overline{z_1} \cdot \frac{1}{\overline{z_2}} \\&= \frac{\overline{z_1}}{\overline{z_2}}\end{aligned}$$Terbukti.
Sifat 8
BUKTI
Ambil sebarang $z \in \mathbb{C}$. Tulis $z=a+bi$, dengan $a,b \in \mathbb{R}$. Konjugat dari $z$ adalah $\overline{z}=a-bi$.Dengan menjumlahkan $z$ dan $\overline{z}$, diperoleh$$\begin{aligned}z+\overline{z} &= 2a \\\frac{z+\overline{z}}{2} &= a \\\frac{z+\overline{z}}{2} &= \text{Re }z\end{aligned}$$Dengan mengurangkan $\overline{z}$ dari $z$, diperoleh$$\begin{aligned}z-\overline{z} &= 2bi \\\frac{z-\overline{z}}{2i} &= b \\\frac{z-\overline{z}}{2i} &= \text{Im }z\end{aligned}$$Terbukti.
Contoh 1
Nyatakan bilangan kompleks$$\frac{-1+3i}{2-i}$$dalam bentuk paling sederhana.
Pembahasan
Bilangan kompleks disebut sederhana jika berada dalam bentuk $a+bi$, dengan $a,b \in \mathbb{R}$. Bilangan kompleks pada soal dinyatakan dalam hasil bagi dua bilangan kompleks lainnya. Agar lebih sederhana, penyebutnya harus berupa bilangan real.
Ingat, berdasarkan sifat 2, $z \cdot \overline{z}$ merupakan bilangan real. Jadi, untuk menyederhanakan bilangan kompleks pada soal, kita perlu mengalikan pembilang dan penyebutnya dengan konjugat dari penyebut.
Kalikan pembilang dan penyebut dengan konjugat dari $2-i$, yaitu $2+i$.$$\begin{aligned}\frac{-1+3i}{2-i} &= \frac{-1+3i}{2-i} \cdot \frac{2+i}{2+i} \\&= \frac{-2-3+6i-i}{4+1} \\&= \frac{-5+5i}{5} \\&= -1+i\end{aligned}$$
Contoh 2
Buktikan bahwa $z_1 \cdot \overline{z_2}+\overline{z_1} \cdot z_2 \in \mathbb{R}$, untuk setiap bilangan kompleks $z_1$ dan $z_2$.
Pembahasan
Ambil sebarang $z_1,z_2 \in \mathbb{C}$. Perhatikan bahwa$$\begin{aligned}\overline{z_1 \cdot \overline{z_2}+\overline{z_1} \cdot z_2} &= \overline{z_1 \cdot \overline{z_2}}+\overline{\overline{z_1} \cdot z_2} \quad \text{[Sifat 4]} \\&= \overline{z_1} \cdot \overline{\overline{z_2}} + \overline{\overline{z_1}} \cdot \overline{z_2} \quad \text{[Sifat 5]} \\&= \overline{z_1} \cdot z_2 + z_1 \cdot \overline{z_2} \quad \text{[Sifat 2]} \\&= z_1 \cdot \overline{z_2}+\overline{z_1} \cdot z_2 \quad \text{[Sifat Komutatif]}\end{aligned}$$Berdasarkan sifat 1, diperoleh $z_1 \cdot \overline{z_2}+\overline{z_1} \cdot z_2 \in \mathbb{R}$.Terbukti.
Contoh 3
Buktikan bahwa $(2+i\sqrt{5})^7+(2-i\sqrt{5})^7 \in \mathbb{R}$.
Pembahasan
Serupa dengan contoh sebelumnya, kita perlu menunjukkan bahwa $(2+i\sqrt{5})^7+(2-i\sqrt{5})^7$ sama dengan nilai konjugatnya. Selain itu, juga diperlukan sifat berikut:
Sifat 9
Sifat ini dapat dibuktikan dengan menggunakan induksi matematika dan sifat 5
Agar lebih sederhana, kita misalkan $2+i\sqrt{5}=z$, sehingga $2-i\sqrt{5}=\overline{z}$. Untuk membuktikan bahwa$$(2+i\sqrt{5})^7+(2-i\sqrt{5})^7 =z^7+\overline{z} \, ^7 \in \mathbb{R}$$kita perlu menunjukkan bahwa $z^7+\overline{z} \, ^7$ sama dengan nilai konjugatnya.Perhatikan bahwa$$\begin{alignedat}{2}\overline{z^7+\overline{z} \, ^7} &= \overline{z^7+\overline{z^7}} \quad &\text{[Sifat 9]} \\&= \overline{z^7}+\overline{\overline{z^7}} \quad &\text{[Sifat 4]} \\&= \overline{z^7}+z^7 \quad &\text{[Sifat 2]} \\&= \overline{z} \, ^7+z^7 \quad &\text{[Sifat 9]} \\&= z^7+\overline{z} \, ^7 \quad &\text{[Sifat Komutatif]}\end{alignedat}$$Berdasarkan sifat 1, diperoleh$$z^7+\overline{z^7}=(2+i\sqrt{5})^7+(2-i\sqrt{5})^7 \in \mathbb{R}$$Terbukti.
