Layang-layang adalah bangun datar empat sisi yang kedua diagonalnya saling tegak lurus. Sepasang sisinya sama panjang, begitu pula dengan sepasang sisi lainnya. Layang-layang memiliki dua buah sudut yang sama besar.
Dalam tulisan ini, kita akan membuktikan rumus luas layang-layang, yaitu$$\text{L} = \frac{1}{2} \cdot \text{diagonal}_1 \cdot \text{diagonal}_2$$
Pembuktian Rumus Luas Layang-Layang
Perhatikan layang-layang ABCD berikut.
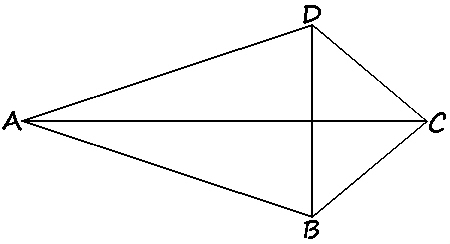
Ruas garis $\text{AC}$ dan $\text{BD}$ adalah diagonal bangun tersebut. Diagonal AC membagi layang-layang menjadi dua buah bangun datar lainnya, yaitu segitiga $\text{ABC}$ dan segitiga $\text{ACD}$.
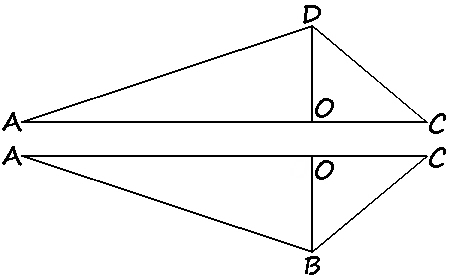
Luas segitiga dapat dihitung dengan rumus $L=\frac{1}{2} \cdot alas \cdot tinggi$. Luas layang-layang sama dengan jumlah luas kedua segitiga.$$\begin{aligned}\text{L ABCD} &= \text{L ABC} + \text{L ACD} \\&= \frac{1}{2} \cdot AC \cdot OB + \frac{1}{2} \cdot \text{AC} \cdot \text{OD} \\&= \frac{1}{2} \cdot \text{AC} \cdot \left( \text{OB} + \text{OD} \right) \\&= \frac{1}{2} \cdot \text{AC} \cdot \text{BD}\end{aligned}$$
Pada layang-layang di atas, $\text{AC}$ dan $\text{BD}$ merupakan diagonal, sehingga terbukti bahwa$$\text{L} = \frac{1}{2} \cdot \text{diagonal}_1 \cdot \text{diagonal}_2$$
