Formula heron atau rumus heron merupakan salah satu rumus untuk menghitung luas daerah segitiga. Rumus ini digunakan jika diketahui panjang ketiga sisi segitiga.
Formula Heron
Rumus ini digunakan sebagai alternatif jika tinggi segitiga belum diketahui, sehingga rumus $L = \frac{1}{2} \cdot \text{alas} \cdot \text{tinggi}$ belum bisa digunakan. Begitupun jika dua sisi dan sudut yang diapit keduanya tidak diketahui.
Ada beberapa cara yang dapat digunakan untuk membuktikan rumus heron. Dalam tulisan ini, kita akan membahas dua di antaranya. Pertama, dengan menggunakan aturan cosinus dan rumus luas segitiga jika besar salah satu sudut diketahui. Kedua, dengan menarik garis tinggi dari salah satu titik sudut segitiga, sehingga terbentuk dua buah segitiga siku-siku. Dengan teorema pythagoras, kita bisa membentuk dua persamaan yang pada akhirnya menghasilkan rumus heron.
Bukti (menggunakan aturan cosinus)
Misal kita akan menentukan luas segitiga dengan panjang sisi $a$, $b$, dan $c$. Sudut yang dibentuk oleh sisi dengan panjang $b$ dan $c$ adalah $\alpha$. Berdasarkan aturan cosinus, kita dapat membentuk persamaan berikut.$$\begin{aligned}a^2 &= b^2 + c^2 {}- 2bc \cdot \cos \alpha \\2bc \cdot \cos \alpha &= b^2 + c^2 {}- a^2 \\\cos \alpha &= \frac{b^2 + c^2 {}- a^2}{2bc}\end{aligned}$$
Misalkan persamaan di atas sebagai persamaan (1). Di lain pihak, kita punya sifat trigonometri di bawah ini.$$\begin{aligned}\sin^2 \alpha + \cos^2 \alpha &= 1 \\\sin^2 \alpha &= 1 {}- \cos^2 \alpha \\\sin^2 \alpha &= (1 + \cos \alpha )(1 {}- \cos \alpha)\end{aligned}$$
Substitusi persamaan (1) pada persamaan di atas.$$\begin{aligned}\sin^2 \alpha &= (1 + \cos \alpha )(1 {}- \cos \alpha) \\&= \left( 1 + \frac{b^2 + c^2 {}- a^2}{2bc} \right) \left( 1 {}- \frac{b^2 + c^2 {}- a^2}{2bc} \right) \\&= \left( \frac{2bc+b^2 + c^2 {}- a^2}{2bc} \right) \left( \frac{2bc-b^2-c^2+a^2}{2bc} \right) \\&= \frac{(2bc+b^2 + c^2 {}- a^2)(2bc-b^2-c^2+a^2)}{(2bc)(2bc)} \\&= \frac{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{(2bc)^2} \\&= \frac{(a+b+c)(a+b+c-2a)(a+b+c-2b)(a+b+c-2c)}{(2bc)^2}\end{aligned}$$
Misalkan $s=\frac{1}{2} (a+b+c)$ atau $2s=a+b+c$, sehingga$$\begin{aligned}\sin^2 \alpha &= \frac{ 2s(2s-2a)(2s-2c)(2s-2b)}{(2bc)^2 } \\&= \frac{16s (s-a) (s-c) (s-b)}{4(bc)^2 } \\&= \frac{4s(s-a)(s-c)(s-b)}{(bc)^2 }\end{aligned}$$
Tarik akar pada kedua ruas$$\begin{aligned}\sin \alpha &= \sqrt{\frac{4s(s-a)(s-c)(s-b)}{(bc)^2 }} \\&= \frac{ \sqrt{4s(s-a)(s-c)(s-b)}}{ \sqrt{(bc)^2} } \\&= \frac{2 \sqrt{s(s-a)(s-c)(s-b)}}{bc}\end{aligned}$$
Misalkan persamaan di atas sebagai persamaan (2).Jika diketahui dua sisi dan sudut yang diapit oleh kedua sisi tersebut, maka luas segitiga dapat dihitung dengan rumus $L = \frac{1}{2}bc \cdot \sin \alpha$.Substitusi persamaan (2) pada rumus di atas, sehingga$$\begin{aligned}L &= \frac{1}{2}bc \cdot \frac{2 \sqrt{s(s-a)(s-c)(s-b)}}{bc} \\&= \sqrt{s(s-a)(s-c)(s-b)}\end{aligned}$$Terbukti.
Bukti (menggunakan teorema pythagoras)
Perhatikan segitiga $\text{ABC}$ berikut.

Lukis garis tinggi segitiga dari titik sudut $\text{A}$. Misalkan perpotongan antara garis tinggi dengan sisi $\text{BC}$ adalah $\text{D}$. Misalkan pula panjang sisi $\text{BD}$ adalah $\text{d}$, sehingga panjang sisi $\text{CD}$ adalah $a-d$.
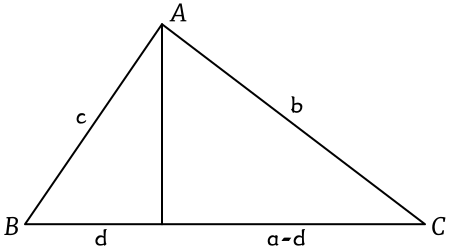
Dengan menggunakan teorema pythagoras pada segitiga $\text{ABD}$ dan $\text{ADC}$, diperoleh$$\begin{aligned}\text{AD}^2 &= \text{AB}^2-\text{BD}^2 \\t^2 &= c^2-d^2\end{aligned}$$dan$$\begin{aligned}\text{AD}^2 &= \text{AC}^2-\text{CD}^2 \\t^2 &= b^2-(a-d)^2 \\&= b^2-(a^2 + d^2-2ad) \\&= b^2-a^2-d^2 + 2ad) \\\end{aligned}$$
Berdasarkan kedua persamaan di atas, diperoleh$$\begin{aligned}c^2-d^2 &= b^2-a^2-d^2 + 2ad \\c^2 &= b^2-a^2 + 2ad) \\2ad &= c^2-b^2 + a^2 \\d &= \frac{c^2-b^2 + a^2}{2a}\end{aligned}$$
Substitusi nilai $d$ pada persamaan $t^2 = c^2-d^2$.$$\begin{aligned}t^2 &= c^2-d^2 \\&= c^2-\left( \frac{c^2-b^2 + a^2}{2a} \right)^2 \\&= c^2-\frac{(c^2-b^2 + a^2)^2}{(2a)^2} \\&= \frac{2a^2c^2-(c^2-b^2 + a^2)^2}{(2a)^2} \\&= \frac{(2ac)^2-(c^2-b^2 + a^2)^2}{(2a)^2} \\&= \frac{(2ac+(c^2-b^2 + a^2))(2ac-(c^2-b^2 + a^2))}{(2a)^2} \\&= \frac{(2ac+c^2-b^2 + a^2)(2ac-c^2+b^2-a^2))}{(2a)^2} \\&= \frac{(a+b+c)(a-b+c)(-a+b+c)(a+b-c)}{(2a)^2} \\&= \frac{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}{(2a)^2} \\&= \frac{(a+b+c)(a+b+c-2a)(a+b+c-2b)(a+b+c-2c)}{(2a)^2}\end{aligned}$$
Diketahui bahwa $s=\frac{1}{2} (a+b+c)$ atau $2s=a+b+c$, sehingga$$\begin{aligned}t^2 &= \frac{ 2s(2s-2a)(2s-2c)(2s-2b)}{(2a)^2 } \\&= \frac{16s (s-a) (s-c) (s-b)}{4a^2 } \\&= \frac{4s(s-a)(s-c)(s-b)}{a^2 }\end{aligned}$$
Tarik akar pada kedua ruas$$\begin{aligned}t &= \sqrt{\frac{4s(s-a)(s-c)(s-b)}{a^2 }} \\&= \frac{ \sqrt{4s(s-a)(s-c)(s-b)}}{ \sqrt{a^2} } \\&= \frac{2 \sqrt{s(s-a)(s-c)(s-b)}}{a}\end{aligned}$$
Luas segitiga $\text{ABC}$ dapat dihitung dengan rumus$$\begin{aligned}L &= \frac{1}{2} \cdot \text{BC} \cdot \text{AD} \\&= \frac{1}{2} \cdot a \cdot t \\&= \frac{1}{2} \cdot a \cdot \frac{2 \sqrt{s(s-a)(s-c)(s-b)}}{a} \\&= \sqrt{s(s-a)(s-c)(s-b)}\end{aligned}$$Terbukti.
