Trapesium merupakan bangun datar yang memiliki empat sisi. Sepasang sisinya sejajar, namun tidak mesti sama panjang. Dalam tulisan ini, kita akan membuktikan rumus luas trapesium. Jika $t$ menyatakan tinggi trapesium, serta $a$ dan $b$ menyatakan sisi-sisi sejajar pada trapeisum, maka luas trapesium dapat dihitung dengan rumus berikut.$$\text{L} = \frac{1}{2} \cdot \text{jumlah sisi sejajar} \cdot \text{tinggi}=\frac{1}{2} \cdot (a+b) \cdot t$$
Pembuktian rumus luas trapesium dibagi menjadi tiga kasus, berdasarkan jenisnya.
Pembuktian Rumus Luas Trapesium Sama Kaki
Perhatikan trapesium sama kaki berikut.
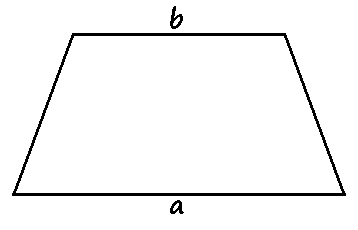
Buat diagonal yang membagi trapesium menjadi dua buah segitiga.

Luas trapesium sama dengan jumlah luas kedua segitiga. Luas segitiga dapat dihitung dengan rumus $\text{L} = \frac{1}{2} \cdot \text{alas} \cdot \text{tinggi}$.$$\begin{aligned}\text{L Trapesium} &= \text{L}_1 + \text{L}_2 \\&= \frac{1}{2} \cdot a \cdot t + \frac{1}{2} \cdot b \cdot t \\&= \frac{1}{2} \cdot t \cdot (a + b)\end{aligned}$$
Pada trapesium di atas, $a$ dan $b$ merupakan sisi sejajar. Dengan demikian, terbukti bahwa.$$\text{L} = \frac{1}{2} \cdot \text{jumlah sisi sejajar} \cdot \text{tinggi}$$
Pembuktian Rumus Luas Trapesium Siku-siku
Perhatikan trapesium siku-siku berikut.
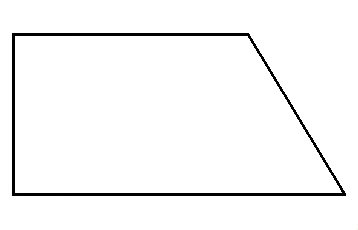
Bagi trapesium tersebut menjadi dua bangun datar, yaitu sebuah persegi panjang dan sebuah segitiga.
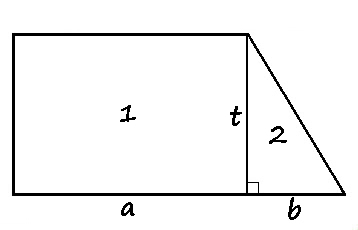
Luas trapesium sama dengan luas persegi panjang ditambah luas segitiga. Luas persegi panjang dapat dihitung dengan rumus $\text{L} = \text{panjang} \cdot \text{lebar}$.$$\begin{aligned}\text{L Trapesium} &= \text{L}_1 + \text{L}_2 \\&= a \cdot t + \frac{1}{2} \cdot b \cdot t \\&= \frac{1}{2} \cdot t \cdot (2a + b)\end{aligned}$$
Pada trapesium di atas, $2a + b$ merupakan jumlah sisi sejajar. Dengan demikian, terbukti bahwa.$$\text{L} = \frac{1}{2} \cdot \text{jumlah sisi sejajar} \cdot \text{tinggi}$$
Pembuktian Rumus Luas Trapesium Sembarang
Perhatikan trapesium sembarang berikut.
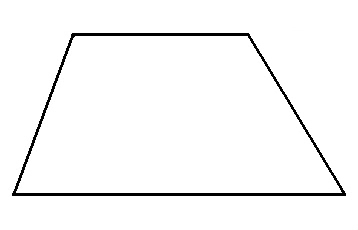
Bagi trapesium tersebut menjadi tiga bangun datar, yaitu sebuah persegi panjang dan dua buah segitiga.
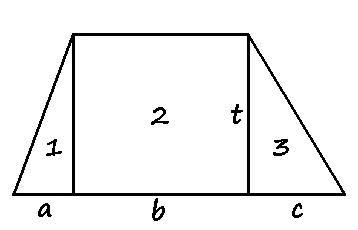
$$\begin{aligned}\text{L Trapesium} &= \text{L}_1 + \text{L}_2 + \text{L}_3 \\&= \frac{1}{2} \cdot a \cdot t + b \cdot t + \frac{1}{2} \cdot c \cdot t \\&= \frac{1}{2} \cdot t \cdot (a + 2b + c)\end{aligned}$$
Pada trapesium di atas, $a + 2b + c$ adalah jumlah sisi sejajar. Dengan demikian, terbukti bahwa$$\text{L} = \frac{1}{2} \cdot \text{jumlah sisi sejajar} \cdot \text{tinggi}$$
